- Dr. Orna

- Jan 17, 2022
- 2 min read
On Saturday, January 15, an underwater volcano erupted near Tonga and was likely the biggest underwater eruption recorded on our planet in more than 30 years. The eruption caused Tsunami waves across the Pacific Ocean that reached the western coast of the US.
The eruption was captured from space in real time as a huge cloud of ash, gas, and steam spewed 12.5 miles (!!) into the atmosphere!

Satellite images from JMA show the volcano eruption in Tonga on January 15.
Can you say "Hunga-Tonga-Hunga-Ha'apai"?
Tonga is a south pacific kingdom made out of more than 170 islands. About100,000 people call it home.
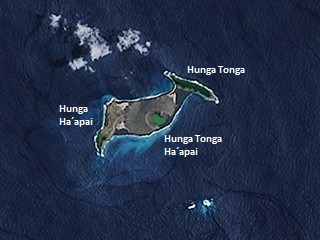
Hunga-Tonga-Hunga-Ha'apai is one of Tonga's islands, and it is a volcanic island.
The volcano itself is an underwater volcano that reaches sea level in 2009 after a volcanic eruption. It lies between two islands: Hunga Tonga and Hunga Haʻapai.
Above from left to right - Tonga's location, Tonga and the underwater volcano, Hunga Tonga-Hunga Haʻapai island
What is an Underwater Volcano?
Underwater Volcanoes or Submarine Volcanoes are underwater vents in the Earth's surface from which magma can erupt. Most underwater volcanoes are very deep but some exist in shallow water and can send material into the atmosphere during an eruption.
Above - Hunga Tonga eruption early on 15 January 2022, taken from the GOES-17 geostationary weather satellite positioned above the equator at 137.2°W longitude.
What is a Tsunami
A Tsunami is a Japanese word that means "harbor wave." It is one of nature's forces.
It is a large wave caused by movements in Earth's outer layer, or crust, which move ocean water. A Tsunami can speed across the ocean as fast as a jet plane. An earthquake, or a volcano eruption in the ocean, can cause a Tsunami.
If a volcano erupts in the ocean, the lava flowing out of the volcano takes up the space of the water around it. That water has to move and it can turn into a large wave. The bigger the volcanic eruption, the bigger the wave of water would be. When the wave reaches the shore, it grows taller because the ocean is shallower.
How do we know if a Tsunami is on its way?
After an oceanic earthquake or underwater volcanic eruption, a Tsunami warning is issued.
NASA has a tool called MISR (the Multi-angle Imaging SpectroRadiometer) that watches for Tsunamis from space. MISR can see sunlight reflecting off waves and measure their height.

Above: The MISR instrument on the Terra satellite takes pictures from different angles to look for tsunamis. Credit: NASA/JPL/Shigeru Suzuki and Eric M. De Jong, Solar System Visualization Project
So what Happened after the Hunga-Tonga-Hunga-Ha'apai eruption?
The eruption caused a Tsunami on Tonga's largest island, Tongatapu, with 4 feet high waves that flooded large areas.
Tsunami warnings went into effect across many Pacific Islands, parts of New Zealand, and as far as Japan, Peru and the United States' + Canada's pacific coast.
The eruption sent waves to the US West Coast, with some exceeding 3 and 4 feet in height, according to the National Weather Service. Tsunami waves were felt in California, Alaska and Hawaii.

Above - A tsunami has hit Tonga's largest island, Tongatapu.
Vocabulary
Underwater Volcano - volcanoes which are under the surface of the world's oceans
Tsunami - a large ocean wave usually caused by an underwater earthquake or a volcanic explosion